| 들어가며
지난 블로깅에는 가우스 소거법에 대해 배웠다.
지난 블로깅의 링크는 아래를 참고한다.
▶ 가우스 소거법(Gaussian elimination)의 이해 - 선형대수 2-2강
이번 블로깅에서는 가우스 조르단 소거법(Gauss Jordan Elimination)에 대해 이해해보자
| 가우스 조르단 소거법이란
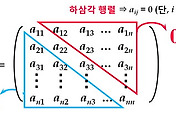
일차 연립방정식 AX = B를 쉽게 풀 수 있는 가우스-조르단 소거법은 다음의 순서를 따른다.
1) 행렬 A와 B로 부터 확대행렬 C=(A|B) 를 구한다.
2) 기본행연산을 이용하여 C를 소거행제형 D로 변환한다.
3) 자유변수 각각을 임의의 매개변수로 둔다.
4) 행렬 D의 영행이 아닌 각 행을 선도변수에 관하여 푼다.
이를 이용해서 다음의 연립방정식을 풀어보자
| 가우스 소거법(Gauss Elimination)과 가우스-조르단 소거법(Gauss Jordan Elimination)의 비교
- 가우스 소거법은 행제형행렬을 구한 다음에 후진 대입법을 사용하여 값을 구한다.
- 가우스 조르단 소거법은 소거행제형 행렬을 구해서 바로 해를 구한다.
| 참고자료
방송통신대학교 강의교재
'기계학습 > 선형대수이론' 카테고리의 다른 글
| 행렬의 곱, 거듭제곱, ,전치 - 선형대수 3-2강 :: Data 쿡북 (0) | 2017.09.11 |
|---|---|
| 행렬의 개요 - 선형대수 3-1강 :: Data 쿡북 (0) | 2017.09.11 |
| 가우스 소거법(Gaussian elimination)의 이해 - 선형대수 2-2강 :: Data 쿡북 (3) | 2017.09.10 |
| 행제형, 소거행제형의 이해 - 선형대수 2-1강 :: Data 쿡북 (0) | 2017.09.10 |
| 확대행렬(Augmented matrix)과 기본행연산(elementary row operation) 그리고 기호 이해 - 선형대수 2강 :: Data 쿡북 (2) | 2017.09.10 |

댓글